Μετατροπές μεγεθών σε ταψιά και άλλα σκεύη φούρνου (μέρος Α)

Τρέπουμε το μέγεθος του στρογγυλού μας σε τετράγωνο ή ορθογώνιο και αντίστροφα!

Πολλές φορές διαβάζουμε σε μια συνταγή για πίτα ή κέικ ή για φαγητό με κρέμα συγκεκριμένης ποσότητας, ότι χρειάζεται ένα μέγεθος ταψιού που δεν υπάρχει στη δική μας κουζίνα. Επειδή λοιπόν πολλές φίλες με ρωτούν πώς να κάνουν μετατροπές και να αλλάξουν το κυκλικό σκεύος που προτείνει η συνταγή σε μακρόστενο ή τετράγωνο, σκέφτηκα να φτιάξω ένα μίνι οδηγό στη σημερινή ανάρτηση. Λόγω ειδικότητας μπορώ να βοηθήσω την κατάσταση.

Μας ενδιαφέρει το σκεύος μας να έχει το ίδιο εμβαδόν βάσης με το προτεινόμενο οπότε υπολογίζουμε το εμβαδόν.

Φυσικά, αν πρόκειται για “ψηλό” παρασκεύασμα (κέικ, παστίτσιο, κλπ) φροντίζουμε να έχει ύψος το σκεύος μας.  Να σημειώσω πρώτα πρώτα πως μετράμε τις διαστάσεις σε εκατοστά (cm) οπότε βρίσκουμε το εμβαδόν σε τετραγωνικά εκατοστά (cm²). Να μη τα γράφω κάθε φορά…

Παίρνουμε μεζούρα, ένα κομπιουτεράκι αν δεν έχουμε ευχέρεια στις πράξεις, και… πάμε!

α) Για τα στρογγυλά:

Η διάμετρος είναι το νούμερο και η ακτίνα (το ρ στον τύπο) είναι το μισό της.

Το εμβαδόν προκύπτει  με τον τύπο Ε=3,14 ∙ ρ² .  Το ρ είναι η ακτίνα του, δηλαδή το μισό του νούμερου ( Το νούμερο των ταψιών δηλώνει διάμετρο δ ). Στο 24άρι  λοιπόν η ακτίνα είναι 12, στο 26 είναι 13, στο 28άρι είναι 14 και ούτω κάθε εξής. Για όσες και όσους το έχουν ξεχάσει, ρ²= ρ∙ρ οπότε…

Για το 20: Ε=3,14∙ 100= 314

Για το 24:  Ε= 3,14∙ 144 = 452,16

Για το 26:  Ε= 3,14∙ 169 = 530,66

Για το 28:  Ε= 3,14 ∙ 196 = 615,44

Γενικά, πολλαπλασιάζουμε την ακτίνα με τον εαυτό της και ό,τι βρούμε με 3,14

β) Πάμε τώρα στα ορθογώνια:

Το εμβαδόν προκύπτει από το γινόμενο των διαστάσεών τους, δηλαδή Ε= α∙β

Οπότε το μόνο που έχουμε να κάνουμε είναι να πολλαπλασιάσουμε τα μήκη των πλευρών του.

Για τα συνηθισμένα λοιπόν ταψάκια έχουμε:

Με διαστάσεις    20Χ30   είναι Ε= 600

Για                       25Χ20   είναι Ε= 500

Για                       15Χ25   είναι Ε=375

Το ταψάκι της ηλεκτρικής κουζίνας είναι συνήθως 36Χ45 δηλαδή 1620 τετρ. εκατοστά και αντιστοιχεί σε 46 νούμερο στρογγυλό (που συχνά δεν το χωράνε οι συνήθεις κουζίνες!).

Γενικά, μετράμε μήκος και πλάτος και τα πολλαπλασιάζουμε.

γ) Για τα τετράγωνα:

Τα πράγματα  πολύ απλά, το εμβαδόν δίνεται από τον τύπο Ε= α² δηλαδή το μόνο που έχουμε να κάνουμε είναι να πολλαπλασιάσουμε την πλευρά επί τον εαυτό της.

Οπότε για τα συνήθη τετράγωνα σκεύη έχουμε:

Με πλευρά 30 εκατοστά 30∙ 30 = 900

Με πλευρά 25 εκατοστά: 25∙25 = 625

Με πλευρά 20 εκατοστά  20∙ 20 = 400

Με πλευρά 16 εκατοστά  16∙ 16 = 256

δ) Για τα οβάλ σκεύη:

Τα πράγματα είναι κάπως πιο σύνθετα, αλλά προσεγγιστικά υπολογίζουμε το εμβαδόν τους σαν να ήταν ελλείψεις (που δεν είναι ακριβώς…). Στην έλλειψη έχουμε δύο άξονες (το μέγιστο μήκος, και το μέγιστο πλάτος) και για να υπολογίσουμε το εμβαδόν της πολλαπλασιάζουμε τα μισά τους (ημιάξονες τα λέμε στα μαθηματικά αλλά εδώ δεν μας ενδιαφέρει το όνομά τους)  και ό,τι βρούμε με 3,14. Το εμβαδόν δίνεται από τον τύπο: Ε = 3,14∙α∙β όπου  α και β οι ημιάξονες.

Δηλαδή σε ένα οβάλ σκεύος με μέγιστο μήκος 30 και μέγιστο πλάτος 20 θα κάνουμε τον πολλαπλασιασμό 15Χ10Χ3,14 = 371

Για ένα συνηθισμένο οβάλ πυρέξ 40Χ28 θα έχουμε 20Χ14Χ3,14=879

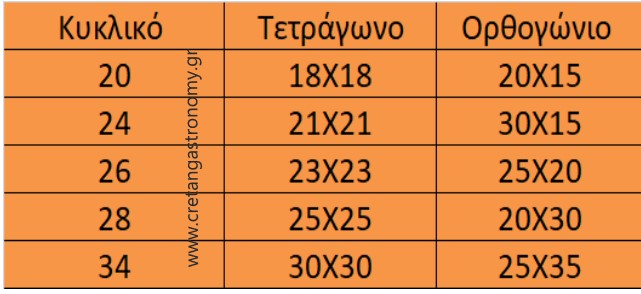
Εύκολα διαπιστώνουμε πως μπορούμε να αλλάξουμε ένα στρογγυλό ταψί μεγέθους 28, με ένα ορθογώνιο 20Χ30 ή με ένα τετράγωνο 25Χ25. Επίσης ένα στρογγυλό ταψί 30 νούμερο μπορεί να πάρει τη θέση ενός πυρέξ 40Χ28

Ας δούμε λοιπόν έναν ενδεικτικό συνοπτικό πίνακα (οι διαφορές μέχρι 30-50 τετραγωνικά εκατοστά δεν επηρεάζουν αισθητά το ύψος των παρασκευασμάτων μας). Έτσι μπορούμε να αντικαθιστούμε το ένα με το άλλο χωρίς αισθητές συνέπειες.

Πάμε τώρα να το δούμε πιο γενικά. Λέει π.χ. μια συνταγή: σκεύος 32Χ15. Πώς το μετατρέπουμε σε στρογγυλό; Έχουμε και λέμε (κομπιουτεράκι εδώ, βαριόμαστε)…  32Χ15 = 480

Διαιρούμε με 3,14 και έχουμε 480: 3,14 =152, 866… και ένα σωρό άλλα δεκαδικά ψηφία που δεν μας ενδιαφέρουν εδώ. Μετά πατάμε το σύμβολο  της τετραγωνικής ρίζας (όλα τα κομπιουτεράκια το έχουν πια).

και βρίσκουμε 12,3. Αυτό όμως είναι ακτίνα και το μέγεθος μας το λέει η διάμετρος. Πατάμε Χ2 και έχουμε τη διάμετρο του κυκλικού σκεύους, 24, 6! Ε τώρα , 25άρι ή 24άρι βάλουμε, μικρή θα είναι η διαφορά!

Το αντίστροφο τώρα!

Συστήνει η συνταγή κυκλικό ταψί μεγέθους 36. Διάμετρος είναι αυτό το νούμερο είπαμε, άρα η ακτίνα του είναι 18. Έχουμε και λέμε (κομπιουτεράκι βεβαίως βεβαίως…) 18Χ18Χ 3,14 =1017,36 Πατάμε πάλι τετραγωνική ρίζα και βρήκαμε την πλευρά του αντίστοιχου τετράγωνου 31,89. Ε τώρα και 32 να είναι δεν χάθηκε ο κόσμος! Και όχι δεν τετραγωνίσαμε τον κύκλο προσεγγίσεις κάνουμε ;-).

Οι φωτογραφίες στο κολάζ είναι από το site https://www.pexels.com/

Σε επόμενο σχετικό άρθρο θα ασχοληθούμε με τη διαδικασία μετατροπής ποσοοτήτων από κανονικό κέικ σε μικρά cup cakes.

Και αν ακόμα μπερδεύεστε, ζητείστε μας με σχόλιο εδώ ή στα social media της σελίδας τη μετατροπή που θέλετε και θα την κάνουμε για σας!